Answer:
a) 209.3 kilojoules must be removed from two liter of beverage, b) A rate of heat removal of 1.163 kilowatts is required to cool down 10 2-liter bottles, c) Cooling 10 2-L bottles during 30 minutes costs 4.9 cents.
Step-by-step explanation:
a) How much heat energy must be removed from your two liters of beverage?
At first we suppose that the beverage has the mass and specific heat of water and that there are no energy interactions between the bottle and its surroundings.
From the First Law of Thermodynamics and definition of sensible heat, we get that amount of removed heat (
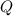 ), measured in kilojoules, is represented by the following formula:
), measured in kilojoules, is represented by the following formula:
 (Eq. 1)
(Eq. 1)
Where:
 - Density of the beverage, measured in kilograms per cubic meter.
- Density of the beverage, measured in kilograms per cubic meter.
 - Volume of the bottle, measured in cubic meters.
- Volume of the bottle, measured in cubic meters.
 - Specific heat of water, measured in kilojoules per kilogram-Celsius.
- Specific heat of water, measured in kilojoules per kilogram-Celsius.
 ,
,
 - Initial and final temperatures, measured in Celsius.
- Initial and final temperatures, measured in Celsius.
If we know that
 ,
,
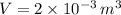 ,
,
 ,
,
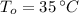 and
and
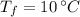 , then:
, then:
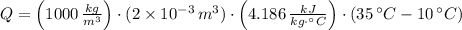
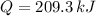
209.3 kilojoules must be removed from two liter of beverage.
b) You are having a party and need to cool 10 of these two-liter bottles in one-half hour. What rate of heat removal, in kW, is required?
The total amount of heat that must be removed from 10 2-L bottles is:
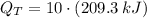
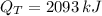
If we suppose that bottles are cooled at constant rate, then, rate of heat removal is determined by this formula:
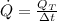 (Eq. 2)
(Eq. 2)
Where:
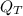 - Total heat, measured in kilojoules.
- Total heat, measured in kilojoules.
 - Time, measured in seconds.
- Time, measured in seconds.
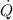 - Rate of heat removal, measured in kilowatts.
- Rate of heat removal, measured in kilowatts.
If we know that
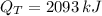 and
and
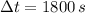 , we find that rate of heat removal is:
, we find that rate of heat removal is:
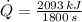

A rate of heat removal of 1.163 kilowatts is required to cool down 10 2-liter bottles.
c) Assuming that your refrigerator can accomplish this and that electricity costs 8.5 cents per kW-hr, how much will it cost to cool these 10 bottles (in $)?
A kilowatt-hour equals 3600 kilojoules. The electricity cost is equal to the removal heat of 10 bottles (
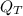 ), measured in kilojoules, and unit electricity cost (
), measured in kilojoules, and unit electricity cost (
 ), measured in US dollars per kilowatt-hour. That is:
), measured in US dollars per kilowatt-hour. That is:
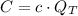
If we know that
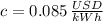 and
and
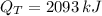 , the total cost of cooling 10 bottles is:
, the total cost of cooling 10 bottles is:

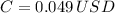
Cooling 10 2-L bottles during 30 minutes costs 4.9 cents.