Given:
Consider the height of the rocket, in feet after x seconds of launch is
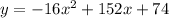
To find:
The time at which the rocket will reach its max, to the nearest 100th of a second.
Solution:
We have,
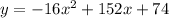
It is a quadratic polynomial with negative leading coefficient. So, it is a downward parabola.
Vertex of a downward parabola is the point of maxima.
To find the time at which the rocket will reach its max, we need to find the x-coordinate of the vertex.
If a quadratic function is
 , then the vertex is
, then the vertex is
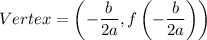
Here,
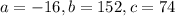 .
.
So,
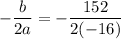
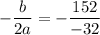
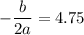
So, x-coordinate of the vertex is 4.75.
Therefore, the rocket will reach its max at 4.75 second.