Answer:
The mean for the probability mass function is 0.64287.
Explanation:
The complete question is:
In a batch of 28 pedometers, 3 are believed to be defective. A quality-control engineer randomly selects 6 units to test. Let random variable X = the number of defective units that are among the units tested.
The probability mass function f (x) is:
f (x) = {(0, 0.47009), (1, 0.42308), (2, 0.10073), (3, 0.00611)}
Solution:
The mean of a discrete random variable X with probability mass function f (x) is:
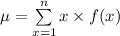
Compute the mean for the probability mass function above as follows:
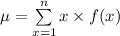
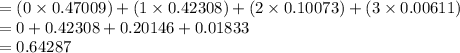
Thus, the mean for the probability mass function is 0.64287.
This values represents the expected number of defective units for every 6 units tested.