Question

The reaction between ethylene and hydrogen bromide to form ethyl bromide is carried out in a continuous reactor. The product stream is analyzed and found to contain 56.7 mol% C2H5Br and 10.3 mol% HBr. The feed to the reactor conains only ethylene and hydrogen bromide. Calculate the fractional conversion of the limiting reactant and the percentage by which the other reactant is in excess. If the molar flow rate of the feed stream is 265 mol/s, what is the extent of reaction

Answer 1

Extent of reaction = 95.9 mol.

Fractional conversion of the limiting reactant = 0.846.

Percentage by which the other reactant is in excess = 25.2 %.

Step-by-step explanation:

Hello.

In this case, for the undergoing chemical reaction:

`CH_2=CH_2+HBr\rightarrow CH_3-CH_2Br`

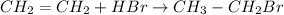
We can write the mole balance per species also including the extent of the reaction:

`CH_2=CH_2:A\\\\HBr: B\\\\CH_3-CH_2-Br:C`

`x_AP=z_AF-\epsilon \\\\x_BP=z_BF-\epsilon \\\\x_CP=\epsilon`

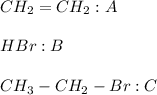
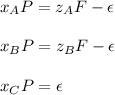
Considering that P is the flow of the outlet product. In such a way, writing the data we know, we can write:

`0.33P=z_A*265-\epsilon \\\\0.103P=z_B*265-\epsilon \\\\0.567P=\epsilon`

Whereas we can replace the C2H5Br mole balance in the others mole balances:

`0.33P=z_A*265-0.567P \\\\0.103P=z_B*265-0.567P\\\\\\z_A*265-0.897P=0\\\\z_B*265-0.67P=0`

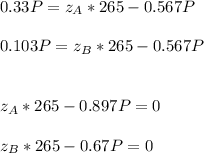
By knowing that
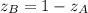`z_B=1-z_A`, we can write:

`z_A*265-0.897P=0\\\\(1-z_A)*265-0.67P=0\\\\\\z_A*265-0.897P=0\\\\-z_A*265-0.67P=-265`

Thus, solving for P and
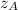`z_A`, we obtain:

`z_A=0.572\\\\P=169.11mol`

It means that the extent of the reaction is:

`\epsilon=0.567P=0.567*169.11mol\\\\\epsilon=95.9mol`

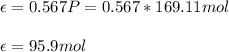
For the limiting reactant, due to the 1:1 mole ratio between the reactants, it is the one having the smallest flow rate:

`F_A=0.572*265mol=151.58mol\\\\F_B=265mol-151.58mol=113.42mol`

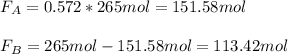
It means that the limiting reactant is B which is HBr, whose fractional conversion is:

`X_B=1-(0.103*169.11)/(113.42mol)\\ \\X_B=0.846`

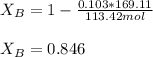
Finally, the percentage by which the other reactant is in excess, corresponds to:

`\% excess =(1-(113.42mol)/(151.58mol))*100\%\\ \\\%excess=25.2\%`

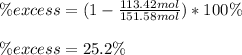
Regards.