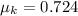Answer:
The coefficient of kinetic friction
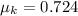
Step-by-step explanation:
From the question we are told that
The length of the lane is
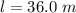
The speed of the truck is

Generally from the work-energy theorem we have that

Here N is the normal force acting on the truck which is mathematically represented as
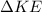 is the change in kinetic energy which is mathematically represented as
is the change in kinetic energy which is mathematically represented as
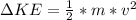
=>
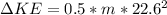
=>
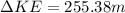

=>
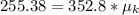
=>