Answer:
(a) 1,411,200.
(b) 302,400.
(c) 100,800.
(d) 1,008,000.
Explanation:
Permutation is the number of ways to select k items from n distinct items in a specific order.
The formula to compute the permutation or arrangement of k items is:
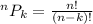
(a)
Compute the total number of schedules as follows:
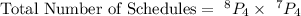
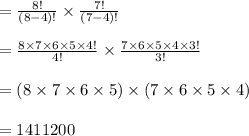
Thus, the total number of schedules are, 1,411,200.
(b)
Compute the number of schedules that includes neither sister as follows:
If neither of sister are included in the schedule then the number of players from the team are 7 and 6 respectively.
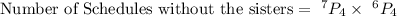
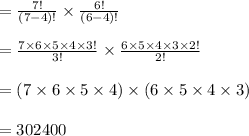
Thus, the number of schedules that includes neither sister is 302,400.
(c)
Compute the number of schedules including both sisters and have them playing against each other as follows:
If both the sisters are playing against each other then there will be three more places to be filled in both the teams.
And the two sisters can play in any of the 4 matches.
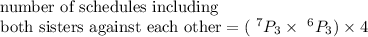
![=[(7!)/((7-3)!)* (6!)/((6-3)!)]* 4\\\\=[( 7* 6* 5* 4!)/(4!)* ( 6* 5* 4* 3!)/(3!)]* 4\\\\=[(7* 6* 5)* (6* 5* 4)]* 4\\\\=100800](https://img.qammunity.org/2021/formulas/mathematics/college/uaxrvwgad9gn333v1jpq5fnte2jyozznbu.png)
Thus, the number of schedules including both sisters and have them playing against each other is 100,800.
(d)
Compute the number of schedules including both sisters as follows:

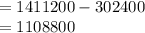
Now compute the number of schedules having the sisters playing in different matches as follows:
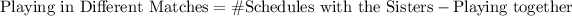
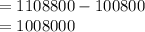
Thus, the number of schedules including both sisters, but have them playing in different matches is 1,008,000.