Given:
The distance s (in feet) of the ball from the ground after t seconds is
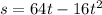
To find:
(a) At what time t will the ball strike the ground?
(b) For what time t is the ball more than 48 feet above the ground?
Solution:
(a)
We have,
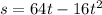
Substitute s=0, to find the time t when the ball strike the ground.

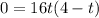
Using zero product property, we get
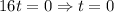
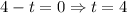
Therefore, the ball strike the ground in initial condition (t = 0) and after 4 seconds (t = 4).
(b)
Now, s > 48, to find the time t when the ball will be more than 48 feet above the ground.
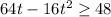
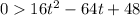
Divide both sides by 16.

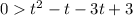

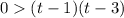
Related equation is
 . Zeroes are t=1,3. These two number divide the number line is three parts. (-∞,1),(1,3),(3,∞)
. Zeroes are t=1,3. These two number divide the number line is three parts. (-∞,1),(1,3),(3,∞)
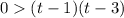 inequality is true for only (1,3).
inequality is true for only (1,3).
It is only possible when t lies in the interval (1,3).
Therefore, the ball will be more than 48 feet above the ground between 1 and 3 seconds.