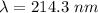Answer:
The value is
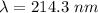
Step-by-step explanation:
From the question we are told that
The slit separation is

The distance of the screen is
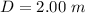
The order of fringe is n = 7
The path difference is
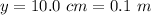
Generally the path difference is mathematically represented as
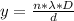
=>

=>

=>

=>
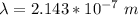
=>