Question

I need help to find the equation of the line in slope-intercept form pls.

Answer 1

y = x - 60

Explanation:

Choose any two pairs/points on the line. In this case, I chose (80, 20) and (40, -20). After that, I plugged them into the following formula for slope:

`(y_(2) - y_(1) )/(x_(2) - x_(1) )`

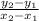
Choose which pair will be pair 2 and which pair will be pair 1. The y's must be always on the top as well and the x's always on the bottom. In this case, I chose (80, 20) to be pair 2 and (40, -20) to be pair 1.

`(20 - (-20))/(80 - 40)`

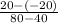
Since a negative and a negative equals a positive, it will be rewritten as:

`(20 + 20)/(80 - 40)`

Once you solve it, you should get
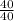`(40)/(40)` which is basically just 1. Your slope is 1, so plug that into the "m," or the slope, in slope-intercept form: y = mx + b. Since we have a 1 for the slope, it can be shown as an invisible 1 so you can just simply write the x. To find b, the y-intercept, look for the point where the line intersects the y-axis. That point is (0, -60). Therefore, your y-intercept is -60. Now, if you write out the entire thing, you now have y = x - 60.

Answer 2

to get the equation of any straight line, we simply need two points off of it, let's use the points from the picture below then.

`(\stackrel{x_1}{-20}~,~\stackrel{y_1}{-80})\qquad (\stackrel{x_2}{40}~,~\stackrel{y_2}{-20}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{-20}-\stackrel{y1}{(-80)}}}{\underset{run} {\underset{x_2}{40}-\underset{x_1}{(-20)}}}\implies \cfrac{-20+80}{40+20}\implies \cfrac{60}{60}\implies 1`

`\begin{array}c \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-80)}=\stackrel{m}{1}(x-\stackrel{x_1}{(-20)}) \\\\\\ y+80=x+20\implies y=x-60`