Question

Please help and explain why you got it right please

Answer 1

A

Explanation:

We want to write the equation of the line as shown in the graph.

First and foremost, we should find the slope of the line. To do so, we will pick two points that the line crosses.

We see that the line crosses the points (0, 5) and (2, -1). Now, we can use the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

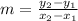
Let (0, 5) be (x₁, y₁) and let (2, -1) be (x₂, y₂). Substitute:

`m=(-1-5)/(2-0)`

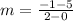
Subtract and reduce. So, our slope is:

`m=-6/2=-3`

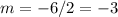
Therefore, our slope is -3.

Now, we can use the point-slope form to find the equation. Point-slope form is:

`y-y_1=m(x-x_1)`

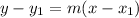
Where m is our slope and (x₁, y₁) is any point the line crosses.

First, since we already know that our slope is -3, let's substitute -3 for m:

`y-y_1=-3(x-x_1)`

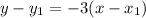
So, we can eliminate choices C and D since the slope of those equations is 3 and not -3.

Now, we need to pick our (x₁, y₁). Let's go through the answer choices A and B to see which one is correct.

For A, we have:

`y+7=-3(x-4)`

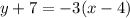
We can rewrite this as:

`y-(-7)=-3(x-(4))`

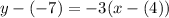
Therefore, in A, our point is (4, -7).

Now, check. Does our line actually pass through (4, -7).

From the graph, we can see that it does. Therefore, A is our correct answer!

However, let's do B just to confirm. For B, we have:

`y+1=-3(x+2)`

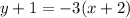
We can rewrite this as:

`y-(-1)=-3(x-(-2))`

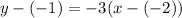
So, our point is (-2, -1).

Does our line pass through (-2, -1)?

Upon inspection, our line does not pass through (-2, -1). So, B is not correct.

So, our answer is A.

And we're done!

Answer 2

y+7 = -3 ( x-4)

Explanation:

First find two points on the graph to find the slope

( 1,2) and ( 3,-4)

The slope is given by

m = ( y2-y1)/(x2-x1)

m = ( -4-2)/(3-1)

= -6/2

=-3

We can use the point slope form

y - y1 = m(x-x1) where m is the slope and x1,y1 is a point on the line

We have two choices with a slope of -3

We can either use and x coordinate of -2 or 4

for -2, the y coordinate is not shown

for 4 , the y coordinate is -7

Using ( 4, -7) and m = -3

y--7 = -3( x- 4)

y+7 = -3 ( x-4)