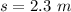Answer:
The distance is
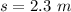
Step-by-step explanation:
From the question we are told that
The frequency of the current is
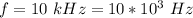
The magnitude of the current is
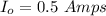
The number of turns is
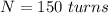
The diameter is
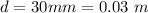
The detection level is
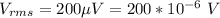
Generally the radius is mathematically represented as
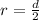
=>
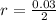
=>
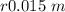
Generally the magnetic field generated by the fence is mathematically represented as
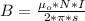
Here s is the point where the do will feel the magnetic field
 is the permeability of free space with value
is the permeability of free space with value
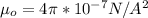
So
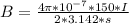
Generally the magnetic flux is mathematically represented as

=>
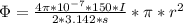
=>
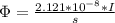
Generally the induced emf is mathematically represented as
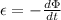
=>

Generally the angular frequency is mathematically represented as
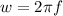
=>
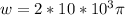
=>

So the current is mathematically represented as
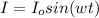
=>
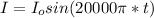
So
![\epsilon =- ( 2.121 *10^(-8) )/( s ) * (d [ I_o sin ( 20000 \pi * t)])/(dt)](https://img.qammunity.org/2021/formulas/physics/college/lvnthzq9rz7hl8aurc836k4hxy17x9st3z.png)
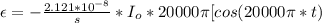
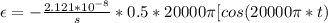
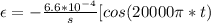
Here the

=>
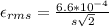
But from the question we are told that
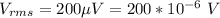
So
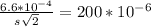
=>
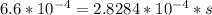
=>