Given:
The function is
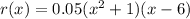
where, function r gives the instantaneous growth rate of a fruit fly population x days after the start of an experiment.
To find:
Number of complex and real zeros.
Time intervals for which the population increased and population deceased.
Solution:
We have,
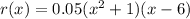
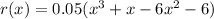
Here, degree of function x is 3. It means, the given function has 3 zeros.
From the given graph it is clear that, the graph of function r(x) intersect x-axis at once.
So, the given function r(x) has only one real root and other two real roots are complex.
Therefore, function r has 2 complex zeros and one real zero.
Before x=6, the graph of r(x) is below the x-axis and after that the graph of r(x) is above the x-axis.
Negative values of r(x) represents the decrease in population and positive value of r(x) represents the increase in population.
Therefore, based on instantaneous growth rate, the population decreased between 0 and 6 hours and the population increased after 6 hours.