Question

If the value of two integers differs by 3, and the product of the two integers is 108, what is the sum of the two integers?

A.21
B.19
C.25 D.23

Answer 1

A

Explanation:

Let the smallest number be n.

If the next integer differs by 3 then:

n + 3 is our second integer.

If the product is 108 then we would multiply them together.

n * (n + 3) = 108 Now solve for n.

(n*n) + (n*3) = 108

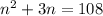`n^(2) +3n = 108` Now we move 108 to the other side by subtracting so we can factor.

`n^(2) + 3n - 108 = 0`

(n )(n ) = 0

Find all the multiples of 108

1 x 108

2 x 54

3 x 36

4 x 27

6 x 18

9 x 12

Which one can we add or subtract together to get 3?

9 x 12 because 12 - 9 = 3

`n^(2) + 3n - 108 = 0`

(n 12)(n 9) = 0 Now we figure out the signs. Since we have -108 one must be negative, and the 3 in the 2nd term (3n) is positive so:

(n + 12)(n - 9) = 0 Is our factored equation.

Our smallest number is 9, so n = 9

Our second number is n + 3 and 9 + 3 = 12

So our 2 integers are 9, 12, there sum would be 9 + 12 = 21

Option A.