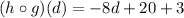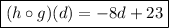Answer:
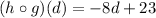
Explanation:
Composite Function
Given g(d) and h(d) real functions, the composite function named (hog)(d) is defined as:
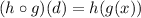
For practical purposes, it can be found by substituting g into h.
The functions g and h are given as:
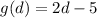
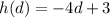
Substituting g into h:
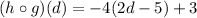
Operating: