Question

Expand the logarithm fully using the properties of logs. Express the final answer in

terms of log .
log 6x^4

Answer 1

P=log(2)+log(3)+4.log(x)

Explanation:

To solve the problem, we need to recall the following properties of the logarithms:

`log(x.y)=log(x)+log(y)`

`log(x^y)=y.log(x)`

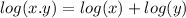
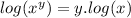
We have the expression:

`P=log(6x^4)`

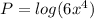
Factor 6=2*3:

`P=log(2\cdot 3x^4)`

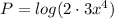
Apply the property of the product:

`P=log(2)+log(3)+log(x^4)`

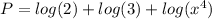
Now apply the property of the exponent:

P=log(2)+log(3)+4.log(x)