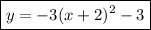Question

Help!!! What is the equation of the following function? Show any work.

Answer 1

`y=-3(x+2)^2-3`

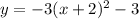
Explanation:

Equation of the Quadratic Function

The vertex form of the quadratic function has the following equation:

`y=a(x-h)^2+k`

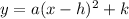
Where (h, k) is the vertex of the parabola that results when plotting the function, and a is a coefficient different from zero.

The graph provided in the question, assumed as a parabola, has two clear points:

The vertex, located at (-2,-3)

The point (-1,-6)

Substituting the coordinates of the vertex, the equation of the function is:

`y=a(x-(-2))^2-3`

`y=a(x+2)^2-3`

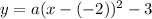
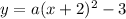
The value of a will be determined by using the other point (-1,-6):

`-6=a(-1+2)^2-3`

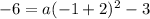
Operating:

`-6=a(1)-3`

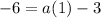
Solving:

a=-3

The equation of the graph is:

`\boxed{y=-3(x+2)^2-3}`