Answer:
The 95% confidence interval estimate for the population mean force is (1691, 1755).
Explanation:
According to the Central Limit Theorem if we have an unknown population with mean μ and standard deviation σ and appropriately huge random samples (n > 30) are selected from the population with replacement, then the distribution of the sample mean will be approximately normally.
The sample selected here is n = 30.
Thus, the sampling distribution of the sample mean will be normal.
Compute the sample mean and standard deviation as follows:
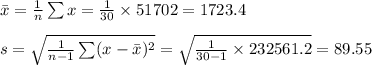
Construct a 95% confidence interval estimate for the population mean force as follows:
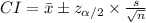

Thus, the 95% confidence interval estimate for the population mean force is (1691, 1755).