Let's see what to do buddy...
_________________________________
Step (1)
Suppose we want to find the sum of numbers from 1 to n.
To do this, we use the following method.
By writing the sum of numbers from 1 to n
, Then we write the sum of numbers n to 1 below it, see :
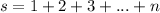
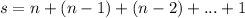
Now we add the sentences of the above two phrases, peer to peer like this :
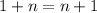
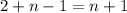

And the others.....
So we have :
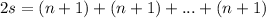
We had n numbers to sum so we have :
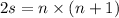
Divided the sides of the equation by 2
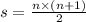
Remember this step I will use it again.
_________________________________
Step (2)
What does the linear sequence mean ?
The linear sequence is the sequence which any terms created by the sum of previous term with constant.
I name that constant value d.
According to above :
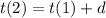
And
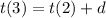
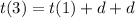

I have a question ;
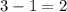
Is it correct ?
If it is correct we have :
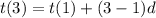
WOW we found a thing ;
Put n instead of 3 :
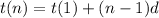
_________________________________
Step (3)
Stop right here.
Let's go to find the sum of the n first terms of the linear sequence.
Do you remember what did we do in step(1) ? Of course you do.
Let's do it again.
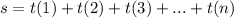

According to the thing what we found in step(2) we have :
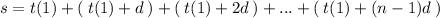
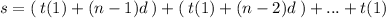
Sum the two above equation's terms like this:
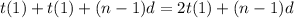
And

And the others like this.
We had n terms so we sumed n terms.
So we have :
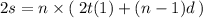
Divided the sides of the equation by 2
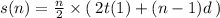
_________________________________
And we're done.
Thanks for watching buddy good luck.
♥️♥️♥️♥️♥️