Question

Point H is on the line segment GI. Given HI=6x, GH=x^2+5x and GI 7x+21. Find the values of x and determine the length of HI.

Answer 1

x=3

HI=18

Explanation:

Equations

Suppose a segment with endpoints G, I. Somewhere in between lies point H, in such a way that:

GI = GH + HI

Every segment is given as an expression with variable x:

`HI=6x`

`GH=x^2+5x`

`GI=7x+21`

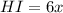
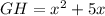
Substituting:

`7x+21=x^2+5x+6x`

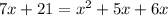
Moving everything to the right side:

`0=x^2+5x+6x-7x-21`

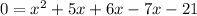
Swapping sides and simplifying:

`x^2+4x-21=0`

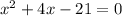
Factoring:

`(x+7)(x-3)=0`

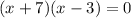
Solving, we have two possible solutions:

x=-7, x=3

The negative solution is discarded because it would result in negative lengths. Thus the solution is

x=3

Determine the length of HI:

HI=6x=6*3=18

HI=18