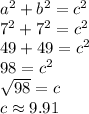Answer:
Explanation:
Since we know the shape is a square, all vertices should be the same length. Find the length of one vertex, by finding the distance between any two points. The following equation uses points
 and
and
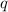 :
:
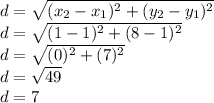
Since the distance is 7, for all sides use the Pythagorean theorem to find the diagonal: