Given that, the total number of students in seventh and eighth grade combined is 584.
The number of students in seventh grade= 5/8 of the total number of students.
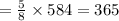
As 4/5 of the total seventh-grade students participated in the track-and-field-event.
So, the number of seventh-grade students participated

The number of students in the eighth grade 3/8 of the total number of students.
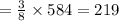
As 7/8 of the total eighth-grade students participated in the track-and-field-event.
So, the number of seventh-grade students participated
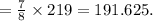
The number of students must be a counting number, but here, as per the given information, the number of seventh-grade students participated coming out a fractional number, so the given information is incorrect.
Although, as per the given data, the mathematical value of the total number of students participated from both the grade combined
=292+191.625
=483.625 (mathematically)
Again, in real life, the fractional value of the total number of students is not possible.