Given:
Amount in Aleka and Helene accounts represented by the following function:
Aleka:
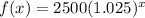
Helene:
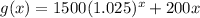
To find:
The function represents the difference,
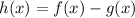 , between the value of Aleka's and Helene's total savings after x years.
, between the value of Aleka's and Helene's total savings after x years.
Solution:
We have,
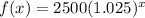
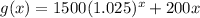
Now,
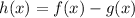
![h(x) = 2500(1.025)^x-[1500(1.025)^x + 200x]](https://img.qammunity.org/2021/formulas/mathematics/high-school/j8w0qv0e4zmast7vmm2bavpn4w8k2841n0.png)

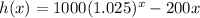
Therefore, the correct option is C.