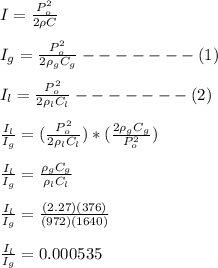Question

(a) If two sound waves, one in a gas medium and one in a liquid medium, are equal in intensity, what is the ratio of the pressure amplitude of the wave in the liquid to that of the wave in the gas? Assume that the density of the gas is 2.27 kg/m3 and the density of the liquid is 972 kg/m3. The speed of sound is 376 m/s in the gas medium and 1640 m/s in the liquid. (b) If the pressure amplitudes are equal instead, what is the ratio of the intensities of the waves (of the one in the liquid to that in the gas)?

Answer 1

(a) The ratio of the pressure amplitude of the waves is 43.21

(b) The ratio of the intensities of the waves is 0.000535

Step-by-step explanation:

Given;

density of gas,
`\rho _g` = 2.27 kg/m³

density of liquid,
`\rho _l` = 972 kg/m³

speed of sound in gas,
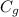`C_g` = 376 m/s

speed of sound in liquid,
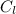`C_l` = 1640 m/s

The of the sound wave is given by;

`I = (P_o^2)/(2 \rho C) \\\\P_o^2 = 2 \rho C I\\\\p_o = √(2 \rho CI)`

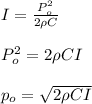
Where;

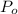`P_o` is the pressure amplitude

`P_o_g= √(2 \rho _g C_gI) -------(1)\\\\P_o_l= √(2 \rho _l C_lI)---------(2)\\\\(P_o_l)/(P_o_g) = (√(2 \rho _l C_lI))/(√(2 \rho _g C_gI)) \\\\(P_o_l)/(P_o_g) = \sqrt{(2 \rho _l C_lI)/(2 \rho _g C_gI) }\\\\ (P_o_l)/(P_o_g) = \sqrt{( \rho _l C_l)/( \rho _g C_g) }\\\\ (P_o_l)/(P_o_g) = \sqrt{( (972)( 1640))/( (2.27)( 376)) }\\\\(P_o_l)/(P_o_g) = 43.21`

(b) when the pressure amplitudes are equal, the ratio of the intensities is given as;

`I = (P_o^2)/(2 \rho C)\\\\I_g = (P_o^2)/(2 \rho _g C_g)-------(1)\\\\I_l = (P_o^2)/(2 \rho _l C_l)-------(2)\\\\(I_l)/(I_g) = ((P_o^2)/(2 \rho _l C_l))*((2\rho_gC_g)/(P_o^2) )\\\\(I_l)/(I_g) = (\rho _gC_g)/(\rho_lC_l) \\\\(I_l)/(I_g) = ((2.27)(376))/((972)(1640))\\\\ (I_l)/(I_g) = 0.000535`