Answer:
1. W = 8848 J
2. W = 7848 J
3. W = 6848 J
Step-by-step explanation:
The work (W) can be found using the following equation:
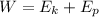
Where: E(k) is the kinetic energy and E(p) is the potential energy
Now let's find the work for every stage.
Stage 1:
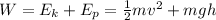
Where: m is the mass, g is the gravity, h is the height, v is the speed
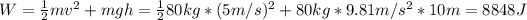
Stage 2:
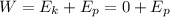
The kinetic energy is equal to zero because the acceleration is constant.
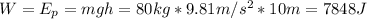
Stage 3:

I hope it helps you!