Question

The lengths of pregnancy terms for a particular species of mammal are nearly normally distributed about a mean pregnancy length with a standard deviation of 7 days. About what percentage of births would be expected to occur within 7 days of the mean pregnancy length

Answer 1

68.268%.

Explanation:

Let \mu be the mean pregnancy length.

The given standard deviation,
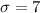`\sigma=7` days

The z-score:

z=\frac{x-\mu}{\sigma}

where x is any pregnancy length.

The range of x within 7 days of the mean pregnancy length is

`\mu-7<x<\mu+7.`

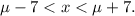
z-score for this range is:

`(\mu-7-\mu)/(\sigma)<z<(\mu+7-\mu)/(\sigma)`

`\Rightarrow -1<z<1`

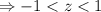
So, the area on the normally distributed curve for the above range of z-score will give the expected percentage of birds to occur within 7 days of the mean pregnancy length.

Now, from the z-score table:

The area from
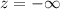`z = -\infty` to z=1 is 0.84134

and the area from
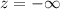`z = -\infty` to z=-1 is 0.15866.

So, the area for -1<z<1

=0.84134 - 0.15866

=0.68268

Hence, the percentage of births would be expected to occur within 7 days of the mean pregnancy length=68.268%.