Question

In the early 1900s, Robert Millikan used small charged droplets of oil, suspended in an electric field, to make the first quantitative measurements of the electron’s charge. A 0.71-um-diameter droplet of oil, having a charge of , is suspended in midair between two horizontal plates of a parallel-plate capacitor. The upward electric force on the droplet is exactly balanced by the downward force of gravity. The oil has a density of 860 kg/m^3 , and the capacitor plates are 4.5 mm apart.

Part A
What must the potential difference between the plates be to hold the droplet in equilibrium?
Express your answer to two significant figures and include the appropriate units

ΔV=

Answer 1

The potential difference is
`\Delta V  =  44.40 \  V`

Step-by-step explanation:

From the question we are told that

The diameter of the droplet of oil is
`d =  0.71 \mu m  =  0.71 *10^(-6) \ m`

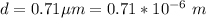
The density of the oil is
`\rho =  860 kg/m^3`

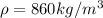
The distance of separation of the capacitor plate is
`l  = 4.5 \ mm =  0.0045 \  m`

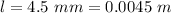
Generally the radius of the droplet is mathematically represented as

`r = (d)/(2)`

=>
`r = (0.71 *10^(-6) )/(2)`

=>
`r = 3.55 *0^(-7) \  m`

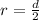
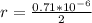
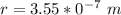
Generally the mass of the oil droplet is mathematically represented as

`m  =  \rho  *  V`

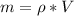
Here V is the volume of the oil droplet which is mathematically represented as

`V  =  (4)/(3) * 3.142 * (3.55 *0^(-7) )^3`

`V  =  1.874 *10^(-19) \  m^3`

So

`m  =  860  *  1.874 *10^(-19)`

=>
`m  =  1.611 *10^(-16) \  kg`

Generally the electric force acting on the droplet is mathematically represented as

`F  =  E  *  q`

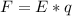
Here q is the charge on an electron with value
`q =  1.60*10^(-19)\ C`

This force is equivalent to the weight of the droplet which is mathematically represented as

`W =  mg`

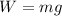
So

`E *  q =  m *  g`

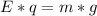
Here E is the electric field which is mathematically represented as

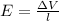
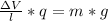
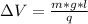
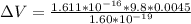
`E =  (\Delta V)/(l)`

`(\Delta V)/(l)  *  q =  m *  g`

=>
`\Delta V  =  (m *  g  *  l )/(q)`

=>
`\Delta V  =  (1.611 *10^(-16)  *  9.8   *  0.0045 )/(1.60*10^(-19))`

=>
`\Delta V  =  44.40 \  V`