Question

A company currently has an advertisement that covers a bill board that is 30 ft wide by 70 ft high. The company wants to reduce the same advertisement to fit on a new billboard that is 25ft wide by 40 ft high. What are the dimensions of the largest advertisement that will fix on the billboard without cropping the advertisement

Answer 1

Given :

A company currently has an advertisement that covers a bill board that is 30 ft wide by 70 ft high. The company wants to reduce the same advertisement to fit on a new billboard that is 25 ft wide by 40 ft high.

To Find :

The dimensions of the largest advertisement that will fix on the billboard without cropping the advertisement.

Solution :

Area of original bill board :

`A_i=30* 70 = 2100\ ft^2`

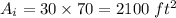
Area of new bill board :

`A_f=25* 40 = 1000\ ft^2`

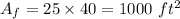
Since, new bill board can be completely fitted in original bill board as its length and breadth both are smaller than that.

So, the dimensions of the largest advertisement that will fix on the billboard without cropping the advertisement is equal to 1000 ft².

Hence, this is the required solution.