The solution to the compound inequality is
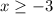 and x < 5, which is represented by option D.
and x < 5, which is represented by option D.
Let's solve the compound inequality step by step:
1. 2x - 3 < 7
Add 3 to both sides:
2x < 10
Divide by 2 (since the coefficient of x is 2 and we want to isolate x):
x < 5
2.

Subtract 5 from both sides:
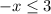
Multiply by -1 (note that when multiplying or dividing by a negative number, the inequality sign flips):
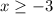
So, the solutions to the compound inequality are x < 5 and
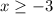 .
.
Now, looking at the answer choices:
C.
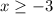 and x < 2 – Incorrect
and x < 2 – Incorrect
D.
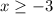 and x < 5 – Correct
and x < 5 – Correct
Therefore, the correct answer is D.
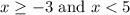 .
.