Answer:
(a) and (b) are not true in general. Refer to the explanations below for counterexamples.
It can be shown that (c) is indeed true.
Explanation:
This explanation will use a lot of empty sets
 just to keep the counterexamples simple.
just to keep the counterexamples simple.
(a)
Note that
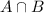 can well be smaller than
can well be smaller than
 . It should be alarming that the question is claiming
. It should be alarming that the question is claiming
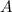 to be a subset of something that can be smaller than
to be a subset of something that can be smaller than
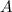 . Here's a counterexample that dramatize this observation:
. Here's a counterexample that dramatize this observation:
Consider:
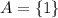 .
.
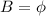 (an empty set, same as
(an empty set, same as
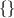 .)
.)
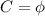 (another empty set.)
(another empty set.)
The intersection of an empty set with another set should still be an empty set:
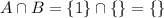 .
.
The union of two empty sets should also be an empty set:
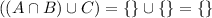 .
.
Apparently, the one-element set
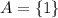 isn't a subset of an empty set.
isn't a subset of an empty set.
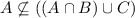 . Contradiction.
. Contradiction.
(b)
Consider the same counterexample
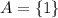 .
.
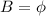 (an empty set, same as
(an empty set, same as
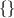 .)
.)
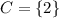 (another empty set.)
(another empty set.)
Left-hand side:
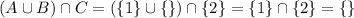 .
.
Right-hand side:
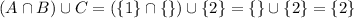 .
.
Apparently, the empty set on the left-hand side
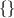 is not the same as the
is not the same as the
 on the right-hand side. Contradiction.
on the right-hand side. Contradiction.
(c)
Part one: show that left-hand side is a subset of the right-hand side.
Let
 be a member of the set on the left-hand side.
be a member of the set on the left-hand side.
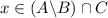 .
.
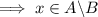 and
and
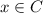 (the right arrow here reads "implies".)
(the right arrow here reads "implies".)
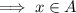 and
and
 and
and
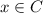 .
.
 and
and
 .
.
 .
.
Note that
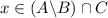 (set on the left-hand side) implies that
(set on the left-hand side) implies that
 (set on the right-hand side.)
(set on the right-hand side.)
Therefore:
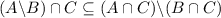 .
.
Part two: show that the right-hand side is a subset of the left-hand side. This part is slightly more involved than the first part.
Let
 be a member of the set on the right-hand side.
be a member of the set on the right-hand side.
 .
.
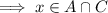 and
and
 .
.
Note that
 is equivalent to:
is equivalent to:
However,
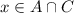 implies that
implies that
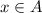 AND
AND
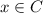 .
.
The fact that
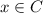 means that the only possibility that
means that the only possibility that
 is
is
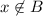 .
.
To reiterate: if
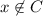 , then the assumption that
, then the assumption that
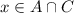 would not be true any more. Therefore, the only possibility is that
would not be true any more. Therefore, the only possibility is that
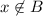 .
.
Therefore,
 .
.
In other words,
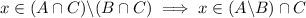 .
.
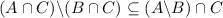 .
.
Combine these two parts to obtain:
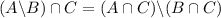 .
.