Answer:

Explanation:
Let's first start by establishing that when it comes to a reflection, side lengths and angle measurements remain the same. With that being said, let's identify our angle measurements:
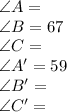
As mentioned earlier, angle measurements will remain the same, so we can go ahead and identify the values of
 &
&
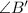
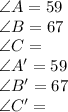
The sum of the angles in a triangle will always be equal to 180°.
Add the two identified angles of the original figure.
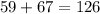
Subtract the sum from 180:
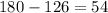
Therefore:

_
Check your work by adding the three identified angle measurements to see if they measure to 180°:
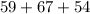
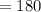
The answer is correct!