Answer:
It will take Rosa 5 and a half (5.5) weeks to have the same amount of money in both accounts.
Explanation:
For this problem, we will have to set two expressions equal to each other. The first expression will represent Rosa's saving account, which already has $117 in it. Every week (
 ), she adds $21 to her savings account:
), she adds $21 to her savings account:
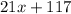
The second expression will represent Rosa's checking account. Rosa's checking account already has $95 in it. Every week (
 ), she adds $25 to her checking account:
), she adds $25 to her checking account:
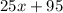
Now that we have our two expressions, set them equal to each other. This is our equation that will be used to find the number of weeks (
 ) it takes until Rosha has the same amount of money in both accounts:
) it takes until Rosha has the same amount of money in both accounts:

Subtract
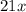 from both sides of the equation:
from both sides of the equation:
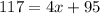
Subtract
 from both sides of the equation:
from both sides of the equation:
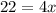
Divide both sides of the equation by the coefficient of
 , which is
, which is
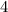 :
:
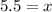

So it will take five and a half weeks for her accounts to have the same amount of money.
_
Check your work by substituting
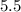 into the initial equation:
into the initial equation:
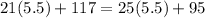
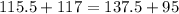

Since the accounts have the same amount, the answer is correct!