Question

Where is the function f(x)=3x^2-6x-45/x^2-5x discontinuous, and what types of discontinuities does it have?

Answer 1

Below.

Explanation:

f(x)=3x^2-6x-45/x^2-5x

= 3x^2-6x-45 / (x(x - 5))

The denominator is zero when x - 0 and x = 5.

So there will be a vertical asymptote at x = 0 and a hole at x = 5.

If we do the division we get f(x) = 3 remainder 9x - 45

so there will also be a horizontal asymptote where x = 3.

Answer 2

Hole at (3, 4.8)

Asymptotes at x = 0 and y = 3

Explanation:

`f(x)=(3x^2-6x-45)/(x^2-5x)`

Factor the numerator:

`\implies 3x^2-6x-45`

`\implies 3(x^2-2x-15)`

`\implies 3(x^2+3x-5x-15)`

`\implies 3(x(x+3)-5(x+3))`

`\implies 3(x-5)(x+3)`

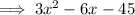
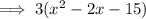
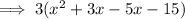
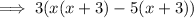
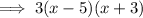
Factor the denominator:

`\implies x^2-5x`

`\implies x(x-5)`

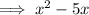
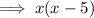
Factored form of function:

`\implies f(x)=(3(x-5)(x+3))/(x(x-5))`

Discontinuity: a point at which the function is not continuous.

Holes

After factoring the rational function, if there is a common factor in both the numerator and denominator, there will be a hole at that point (x-value):

`\implies (x-5)=0 \implies x=5`

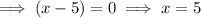
Factor out the common factor from the function and input the found value of x into the new function to find the y-value of the hole:

`\implies f(x)=(3(x+3))/(x)`

`\implies f(5)=(3(5+3))/(5)=4.8`

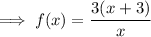
Therefore, there is a hole at (5, 4.8)

Asymptotes

To find the vertical asymptotes, set the denominator of the new (factored) function to zero and solve:

⇒ Vertical Asymptote at x = 0

As the degrees of the leading terms of the numerator and denominator are equal (both x²), the horizontal asymptote is equal to the ratio of the leading coefficients.

⇒ Horizontal Asymptote at y = 3