Question

ANSWER I ADDED EXTRA POINTS BUT ANSWER RIGHT AND EXPLAIN YOUR ANSWER!!!! 2 QUESTIONS...

24.) What is the equation in slope-intercept form of the line that passes through the point (2, -2) and is perpendicular to the line represented by y= 2/5x + 2 ?
A) y= 5/2x - 7
B) y= 5/2x + 7
C) y= -5/2x - 3
D) y= -5/2x + 3
25.) Suppose the linear cost function C(x) = 6x gives the cost for buying x items. If the items are sold in packages of 10, and no one can buy more than 5 packages, then the RANGE of the function C is
A) [0, 50]
B) [5, 10]
C) {0, 6, 12, 18, 24, 30}
D) {0, 60, 120, 180, 240, 300}

Answer 1

24) D

25) D

Explanation:

24) D

We want to find the equation of a line (in slope-intercept form) that passes through (2, -2) and is perpendicular to
`y=(2)/(5)x+2`.

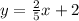First, let's find the slope of our new line.

Remember that perpendicular slopes are negative reciprocals of each other.

Therefore, to find the slope of our new line, we will flip our old slope and add a negative.

Therefore, the slope of our new line is -5/2.

Now, we can use the point-slope form:

`y-y_1=m(x-x_1)`

Where m is the slope and (x₁, y₁) is a point.

So, let's substitute -5/2 for our slope and (2, -2) for our point (x₁, y₁). This yields:

`y-(-2)=-(5)/(2)(x-2)`

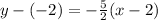
Simplify:

`y+2=-(5)/(2)(x-2)`

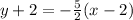
Let's convert this to slope-intercept form. Distribute the right:

`y+2=-(5)/(2)x+5`

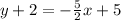
Subtract 2 from both sides. So, our equation is:

`y=-(5)/(2)x+3`

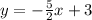
Our answer is D.

25)

We know that the cost for buying x items is given by the function:

`C(x)=6x`

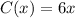
We also know that the items are sold in packages of 10 only. And no one can buy more than 5 packages. In other words, we can buy 0, 1, 2, 3, 4, or 5 packages.

So, let's see how much it will be if we buy 0 packages. This will just be:

`C(0)=6(0)=\$0`

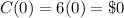
If we buy 1 package, there will be 10 items in them. So:

`C(10)=6(10)=\$60`

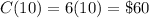
If we do this for 2 packages (20 items), 3 packages (30 items), and so on, we will get:

`C(20)=6(20)=\$120\\C(30)=6(30)=\$180\\C(40)=6(40)=\$240\\C(50)=6(50)=\$300`

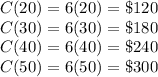
So, our range is:

`\{0, 60, 120, 180, 240, 300\}`

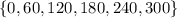
The correct answer is D.

And we're done!