Answer:
It will take 26.34 minutes for the population to reach 5 times its initial value
Explanation:
Exponential Growing
The population of bacteria grows at a rate expressed by the equation:
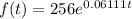
Where t is in minutes.
We need to know when the population will reach 5 times its initial value. The initial value can be determined by setting t=0:
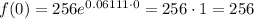
Now we find the time when the population is 5*256=1,280. The equation to solve is:
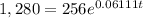
Dividing by 256:
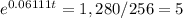
Taking natural logarithms:
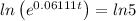
Applying the logarithm properties:
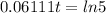
Solving for t:

It will take 26.34 minutes for the population to reach 5 times its initial value