Question

Indicate the equation of the given line in standard form. The line with slope 9/7 and containing the midpoint of the segment whose endpoints are (2, -3) and (-6,5).​

Answer 1

Given parameters:

Coordinates of end points = (2, -3) and (-6,5).​

Slope of line =
`(9)/(7)`

Unknown:

Equation of the line with the given slope = ?

Solution:

Let us find the coordinates of the mid-point of the line given.

Since the end points are (2, -3) and (-6,5);

Midpoint;

x, y =
`(x_(1) + x_(2) )/(2)` ,
`(y_(1) + y_(2) )/(2)`

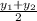
x, y =
`(2 + (-6))/(2)` ,
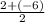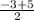`(-3 + 5)/(2)` = -2 , 1

The coordinate of the mid point = -2,1

Equation of a line is;

y = mx + c

x and y are the coordinates

m is the slope

c is the y intercept

We need to find c in order to fully develop our equation;

y = mx + c

y = 1 , x = -2 and m =
`(9)/(7)`

So,

1 =
`(9)/(7)` x (-2) + c

c = 1 +
`(18)/(7)` =
`(25)/(7)`

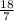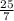
Now, the equation of the line is;

y = -2x +
`(25)/(7)`

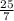
Multiply through by 7,

7y = -14x + 25

The equation of the line is 7y = -14x + 25