Answer:
The number of text messages is 85 ⇒ B
Explanation:
To solve this question
- Assume that the number of the text message is x and the total cost is y
- Make a linear equation represented each plan, then equate their total cost (y) to find the number of the text message (x)
The form of the linear equation is y = m x + b, where
Plan A:
∵ The fee per message is $0.10
∴ m = 0.10
∵ The monthly fee is $35
∴ b = 35
∴ The total cost y = 0.10 x + 35
Plan B:
∵ The fee per message is $0.30
∴ m = 0.30
∵ The monthly fee is $18
∴ b = 18
∴ The total cost y = 0.30 x + 18
∵ Both plans cost is the same for one month
→ Equate the right sides of the two equations
∴ 0.30 x + 18 = 0.10 x + 35
→ Subtract 0.10 x from both sides
∴ 0.30 x - 0.10 x + 18 = 0.10 x - 0.10 x + 35
∴ 0.20 x + 18 = 35
→ Subtract 18 from both sides
∴ 0.20 x + 18 - 18 = 35 - 18
∴ 0.20 x = 17
→ Divide both sides by 0.20
∴
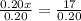
∴ x = 85
∴ The number of text messages is 85