Question

Solve for x in the equation.

Answer 1

The solution is
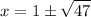`\displaystyle x=1\pm √(47)`. Fourth option

Step-by-step explanation:

Solve for x:

`2x^2+3x-7=x^2+5x+39`

Move all the terms from the right to the left side of the equation, a zero in the right side:

`2x^2+3x-7-x^2-5x-39=0`

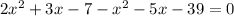
Join all like terms:

`x^2-2x-46=0`

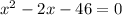
The general form of the quadratic equation is:

`ax^2+bx+c=0`

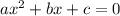
Solve the quadratic equation by using the formula:

`\displaystyle x=(-b\pm √(b^2-4ac))/(2a)`

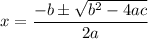
In our equation: a=1, b=-2, c=-46

Substituting into the formula:

`\displaystyle x=(-(-2)\pm √((-2)^2-4(1)(-46)))/(2(1))`

`\displaystyle x=(2\pm √(4+184))/(2)`

`\displaystyle x=(2\pm √(188))/(2)`

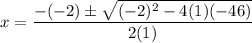
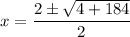
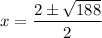
Since 188=4*47

`\displaystyle x=(2\pm √(4*47))/(2)`

Take the square root of 4:

`\displaystyle x=(2\pm 2√(47))/(2)`

Divide by 2:

`\displaystyle x=1\pm √(47)`

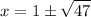
First option: Incorrect. The answer does not match

Second option: Incorrect. The answer does not match

Third option: Incorrect. The answer does not match

Fourth option: Correct. The answer matches exactly this option