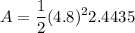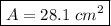Question

Find the area of a sector with a central angle of 140° and a diameter of 9.6 cm. Round to the nearest tenth.

Answer 1

`A=28.1\ cm^2`

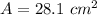
Explanation:

The area of a circular sector with a central angle θ and radius r is given by:

`\displaystyle A=(1)/(2)r^2 \theta`

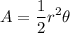
Note: The angle must be in radians.

We need to find both the radius and the angle in radians.

Diameter = 9.6 cm

Radius r=Diameter/2=4.8 cm

Angle in radians= Angle in degrees*π / 180

θ = 140*π / 180 = 2.4435 rad

Now we calculate the area:

`\displaystyle A=(1)/(2)(4.8)^2 2.4435`

`\boxed{A=28.1\ cm^2}`