A. True. We see this by taking the highest order term in each factor:
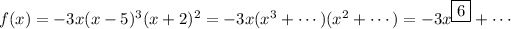
B. True. Again we look at the leading term's degree and coefficient. f(x) behaves like -3x⁶ when x gets large. The degree is even, so as x goes to either ± ∞, x⁶ will make it positive, but multiplying by -3 will make it negative. So on both sides f(x) approaches -∞.
C. False. f(x) = 0 only for x=0, x = 5, and x = -2.
D. False. Part of this we know from the end behavior discussed in part B. On any closed interval, every polynomial is bounded, so that for any x in [-2, 5], f(x) cannot attain every positive real number.
E. True. x = 0 is a root, so f(0) = 0 and the graph of f(x) passes through (0, 0).
F. False. (0, 2) corresponds to x = 0 and f(x) = 2. But f(0) = 0 ≠ 2.