Question

A building's 10th floor (34.5 m high) is blazing with fire. A fire truck arrived at the scene and the fire

men shoots water from their hose. The water leaves the hose at the speed of 29 m/s, at an angle
of
63° and is held at 0.90 m from the ground. Will the water reach the fire? If so, how far from the
building should the hose be so the fire could be put out? ​

Answer 1

Yes, the water will be reach the fire.

The hose should be at 34.7 m from the building

Step-by-step explanation:

Given that,

Height of building's =34.5 m

Speed = 29 m/s

Angle = 63°

Distance from the ground = 0.90 m

We need to calculate the actual height

Using formula of height

`H=(u^2\sin^2\theta)/(2g)`

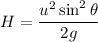
Put the value into the formula

`H=\frac{29^2\sin^2{63}}{2*9.8}`

`H=34.0\ m`

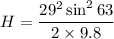
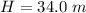
The height from the ground will be

`H'=34+0.90`

`H'=34.9\ m`

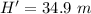
We can say that, the water gun attained the maximum height that is 0.4 m more than the 10th floor.

So, yes, the water will be reach the fire.

We need to calculate the range

Using formula of range

`R=(u^2\sin2\theta)/(g)`

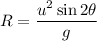
Put the value into the formula

`R=(29^2*\sin(2*63))/(9.8)`

`R=69.4\ m`

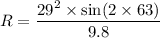
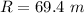
The house should be at half of R.

`(R)/(2)=(69.4)/(2)`

`(R)/(2)=34.7\ m`

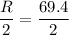
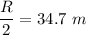
Hence, Yes, the water will be reach the fire.

The hose should be at 34.7 m from the building