Question

1. Using the diagram below, answer the following question. Arthur is at the coordinate A(20,35), Cameron is at the coordinate C(65,40), and Jamie is at the coordinate J(45,20).

Arthur kicks the ball to Cameron in the soccer game. Jamie wants to intercept the ball at the midpoint of the distance between Arthur and Cameron. What is the coordinate of the midpoint that Jamie must run towards? Write your answer as a decimal, if necessary. ​

Answer 1

(42.5, 37.5)

Explanation:

Given:

Arthur = A(20, 35)

Cameron = C(65, 40)

Jamie = J(45, 20)

Required:

Coordinate of the midpoint of the distance between A and C.

SOLUTION:

Midpoint (M) of AC, is given as:

`M((x_1 + x_2)/(2), (y_1 + y_2)/(2))`

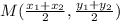
Let
`A(20, 35) = (x_1, y_1)`

`C(65, 40) = (x_2, y_2)`

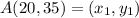
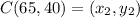
Plug the values into the given formula:

`M((20 + 65)/(2), (35 + 40)/(2))`

`M((85)/(2), (75)/(2))`

`M(42.5, 37.5)`

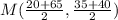
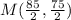
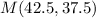
Coordinate Jamie should run towards is (42.5, 37.5)