Answer:
The statement is now presented as:
![\exists\, (h,k)\in \mathbb{R}^(2) /f: (x-h^(2))+(y-k)^(2)=r^(2)\implies f': [x-(h+4)]^(2)+[y-(-k)]^(2) = r^(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ogkfdp4n09gdauwmhtzh9s411skn96tmng.png)
In other words, this mathematical statement can be translated as:
There is a point (h, k) in the set of real ordered pairs so that a circumference centered at (h,k) and with a radius r implies a equivalent circumference centered at (h+4,-k) and with a radius r.
Explanation:
Let
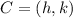 the coordinates of the center of the circle, which must be transformed into
the coordinates of the center of the circle, which must be transformed into
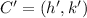 by operations of translation and reflection. From Analytical Geometry we understand that circles are represented by the following equation:
by operations of translation and reflection. From Analytical Geometry we understand that circles are represented by the following equation:

Where
 is the radius of the circle, which remains unchanged in every operation.
is the radius of the circle, which remains unchanged in every operation.
Now we proceed to describe the series of operations:
1) Center of the circle is translated 4 units to the right (+x direction):
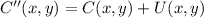 (Eq. 1)
(Eq. 1)
Where
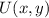 is the translation vector, dimensionless.
is the translation vector, dimensionless.
If we know that
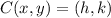 and
and
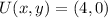 , then:
, then:

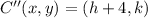
2) Reflection over the x-axis:
![C'(x,y) = O(x,y) - [C''(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/5x8tfy33v3egmekf3da4f7yx0zav2qtp81.png) (Eq. 2)
(Eq. 2)
Where
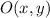 is the reflection point, dimensionless.
is the reflection point, dimensionless.
If we know that
 and
and
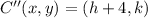 , the new point is:
, the new point is:
![C'(x,y) = (h+4,0)-[(h+4,k)-(h+4,0)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/bp8ztqa81xd20jhnu36udigjip8n6cndn3.png)

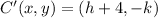
And thus,
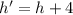 and
and
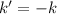 . The statement is now presented as:
. The statement is now presented as:
![\exists\, (h,k)\in \mathbb{R}^(2) /f: (x-h^(2))+(y-k)^(2)=r^(2)\implies f': [x-(h+4)]^(2)+[y-(-k)]^(2) = r^(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ogkfdp4n09gdauwmhtzh9s411skn96tmng.png)
In other words, this mathematical statement can be translated as:
There is a point (h, k) in the set of real ordered pairs so that a circumference centered at (h,k) and with a radius r implies a equivalent circumference centered at (h+4,-k) and with a radius r.