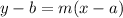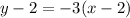Question

The line shown represents the amount of money left on a gift card, y, after Mina buys lattes. After buying 2 lattes, she has $2 left. What is an equation of the line in point- slope form?​

Answer 1

`y - 2 = -3(x - 2)`

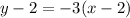
Explanation:

Given that after she buys 2 lattes, she has $2 left, this represents a point on the line in the graph, which is (2, 2).

Point-slope form of equation for a line is given as
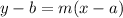`y - b = m(x - a)`. Where,

(a, b) = a point on the line

m = slope

The equation of the line in point-slope form is given by the formula,
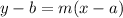`y - b = m(x - a)`, where,

(a, b) = coordinates of a point on the line.

`m = slope = (y_2 - y_1)/(x_2 - x_1)`

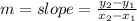
We already have values for (a, b) = (2, 2), let's find the slope (m).

Using (2, 2) and any point on the line, such as (0, 8), we can find the slope as follows:

`m = slope = (y_2 - y_1)/(x_2 - x_1) = (8 - 2)/(0 - 2)`

`= (6)/(-2)`

`m = -3`

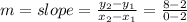
Now we know that a = 2, b = 2 , and m = -3. Let's plug in this values into the point-slope equation as shown below:

`y - b = m(x - a)`

`y - 2 = -3(x - 2)`