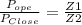Question

Many biological systems are well-described by the laws of statistical physics. A simple yet often powerful approach is to think of a system as having only two states. For example, an ion channel may be open or closed. In this problem, consider a simple model of membrane channels for ions: The system is described by a Boltzmann distribution with only two states, with energies ε1 (open) and ε2 (closed). Assume the "open" state is the state of higher energy, so that ε1 > ε2.

If the probability of finding an ion channel open is popen and the probability of finding the ion channel closed is pclosed, which of the expressions below best represents the relative probability of open to closed, R = popen/pclosed? Use the notation z1 = e-ε1/kBT and z2 = e-ε2/kBT

a. z1-z2
b. z2-z1
c. z1/z2
d. z2/z1
e. Something else

Answer 1

z1/z2

Step-by-step explanation:

we have no quantum effects therefore we can make use of Maxwell Boltzmann distribution in the description of this system.

using the boltzman distribution the probability of finding a particle in energy state

`P_(ei) = (gie^(-ei/kol) )/(z)`

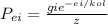
we have

gi to be degeneration of the ith state

ei to be energy of ith state

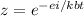`z=e^(-ei/kbt)` summation

`P_(ope) = (e^(-ei/kBt) )/(z) = (Z_(1) )/(Z)`

We have R to be equal to

`(P_(ope) )/(P_(Close) ) = (Z1)/(Z2)`