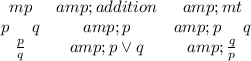Answer:
Follows are the solution to this question:
Step-by-step explanation:
H = It is the half of nation is depressed
J = It is the Insurance, which is provide by the way.
P = It is the phychiatris way
E = An antidepressant drugs, which can be used by everyone
w = The patients want real treatment
Symbolic form can be defined as follows:
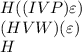
Substance: (IVP)
The evidence:
![i). H \supset ((IVP)\supset \varepsilon ) \\ii). (HVW) \supset \wedge \varepsilon \\iii). H \\iv). (IVP) \supset \varepsilon [ 1,3 Modus Porers] \\v). HVW [ 3 , adddition] \\vi). \wedge \varepsilon [2, 5 mp] \\vii). \wedge (IVP) [4,6 Modus tollens]](https://img.qammunity.org/2021/formulas/social-studies/college/lur26qwh5m58chgwmx1a439rukoxm8thmd.png)
So it's true that conclusion.