The missing figures in the question can be seen below.
The average retirement age = 56.1 years ...
The number of a survey of retired citizen = 49
The standard deviation of the retirement age is 6 years.
Using alpha ∝ = 0.02
Answer:
Explanation:
From the given options in the first question in the given information.
Type I error can take place when the researcher concludes the average retirement age increased, but the average retirement age did not increase.
A Type II error can take place when the researcher concludes that the average retirement age did not increase, but the average retirement age increased.
Recall that:
population mean = 56.1
sample size = 49
standard deviation = 6
At the level of significance of 0.02, using the Excel function (=Normsinv(0.02))
The critical value for z = 2.054
Standard error =

=
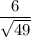
= 6/7
= 0.857
The rejection region
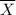 =
=
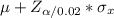
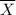 =
=
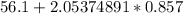
 = 57.86
= 57.86
P(Type II error) is as follows:
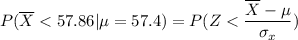
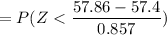
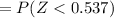
From z tables;
P (Type II error) = 0.704
P(Type II error) is as follows:

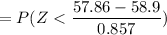
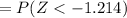
From z tables;
P (Type II error) = 0.1124