Final Answer:
The equation representing the situation is
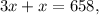 where
where
 is the number of hot dog meals sold. This equation captures the information that the number of pizza meals sold was three times the number of hot dog meals, and the total revenue from the meals amounted to $658.
is the number of hot dog meals sold. This equation captures the information that the number of pizza meals sold was three times the number of hot dog meals, and the total revenue from the meals amounted to $658.
Step-by-step explanation:
Let's denote
 as the number of hot dog meals sold. Given that the number of pizza meals sold was three times the number of hot dog meals, the number of pizza meals sold is
as the number of hot dog meals sold. Given that the number of pizza meals sold was three times the number of hot dog meals, the number of pizza meals sold is
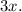 The total revenue from hot dog meals is
The total revenue from hot dog meals is
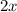 (as each hot dog meal costs $2), and the total revenue from pizza meals is
(as each hot dog meal costs $2), and the total revenue from pizza meals is
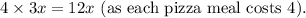
The total revenue from both types of meals is the sum of the revenues from hot dog and pizza meals, expressed as
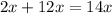 . According to the problem, the total revenue is $658. Therefore, the equation representing the situation is
. According to the problem, the total revenue is $658. Therefore, the equation representing the situation is
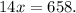
To find the value of
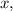 we solve for
we solve for
 by dividing both sides of the equation by 14:
by dividing both sides of the equation by 14:
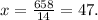 Thus, the number of hot dog meals sold is 47, and the number of pizza meals sold is
Thus, the number of hot dog meals sold is 47, and the number of pizza meals sold is
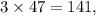 confirming that the number of pizza meals was indeed three times the number of hot dog meals, and the total revenue adds up to $658.
confirming that the number of pizza meals was indeed three times the number of hot dog meals, and the total revenue adds up to $658.
This detailed calculation ensures a clear understanding of the solution to the given problem.