Question

Consider the following hypothetical scenario for Jordan Lake, NC. In a given year, the average watershed inflow to the lake is 900 cfs. Precipitation over the lake is 32 inches/year and evaporation over the lake is 55 inches/year; the area of the lake is 47,000 ac. If an average flow of 300 cfs must be released from the dam for the benefit of fish and downstream water users, calculate the amount of water that can be withdrawn from the lake to provide water supply for the Triangle area. Assume any other source/sink of water (such as groundwater), is negligible.

Answer 1

The lake can withdraw a maximum of
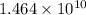`1.464* 10^(10)` cubic feet per year to provide water supply for the Triangle area.

Step-by-step explanation:

The maximum amount of water that can be withdrawn from the lake is represented by the following formula:

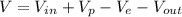`V = V_(in)+V_(p)-V_(e)-V_(out)` (Eq. 1)

Where:

`V` - Available amount of water for water supply in the Triangle area, measured in cubic feet per year.

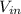`V_(in)` - Inflow amount of water, measured in cubic feet per year.

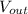`V_(out)` - Amount of water released for the benefit of fish and downstream water users, measured in cubic feet per year.

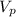`V_(p)` - Amount of water due to precipitation, measured in cubic feet per year.

`V_(e)` - Amount of evaporated water, measured in cubic feet per year.

Then, we can expand this expression as follows:

`V = f_(in)\cdot \Delta t+h_(p)\cdot A_(l)-h_(e)\cdot A_(l)-f_(out)\cdot \Delta t`

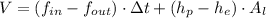`V = (f_(in)-f_(out))\cdot \Delta t +(h_(p)-h_(e))\cdot A_(l)` (Eq. 2)

Where:

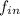`f_(in)` - Average watershed inflow, measured in cubic feet per second.

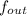`f_(out)` - Average flow to be released, measured in cubic feet per second.

`\Delta t` - Yearly time, measured in seconds per year.

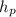`h_(p)` - Change in lake height due to precipitation, measured in feet per year.

`h_(e)` - Change in lake height due to evaporation, measured in feet per year.

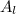`A_(l)` - Surface area of the lake, measured in square feet.

If we know that
`f_(in) = 900\,(ft^(3))/(s)`,
`f_(out) = 300\,(ft^(3))/(s)`,
`\Delta t = 31,536,000\,(second)/(yr)`,
`h_(p) = 32\,(in)/(yr)`,
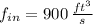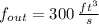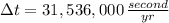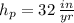`h_(e) = 55\,(in)/(yr)` and
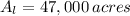`A_(l) = 47,000\,acres`, the available amount of water for supply purposes in the Triangle area is:

`V = \left(900\,(ft^(2))/(s)-300\,(ft^(3))/(s) \right)\cdot \left(31,536,000\,(s)/(yr) \right) +\left(32\,(in)/(yr)-55\,(in)/(yr) \right)\cdot \left((1)/(12)\,(ft)/(in)\right)\cdot (47000\,acres)\cdot \left(43560\,(ft^(2))/(acre) \right)`
`V = 1.464* 10^(10)\,(ft^(3))/(yr)`

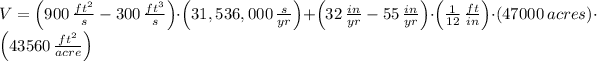
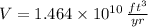
The lake can withdraw a maximum of
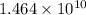`1.464* 10^(10)` cubic feet per year to provide water supply for the Triangle area.