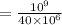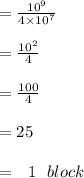Question

Suppose users share a 1-Gbps link. Also, suppose each user requires 200 Mbps when transmitting, but each user only transmits 30 percent of the time.

a. (5 pts.) When circuit switching is used, how many users can be supported?



b. (5 pts.) For the remainder of this problem, suppose packet switching is used. What is the maximum number of users that can be supported if the required blocking probability is strictly less than 0.05 and what is the blocking probability with the determined maximum number of users?

Answer 1

The answer is "5 users and 1 block".

Step-by-step explanation:

In Option a:

Bandwidth total
`= 1-Gbps * 1000`

`= 1,000 \ Mbps`

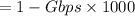
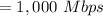
Any User Requirement
`= 200 \ Mbps`

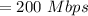
The method for calculating the number of approved users also is:

Now, calculate the price of each person for overall bandwidth and demands,

`\text{Sponsored user amount} = \frac{\text{Bandwidth total}}{\text{Each user's requirement}}`

`=(1000)/(200)\\\\=(10)/(2)\\\\= 5 \ users`

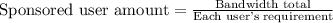
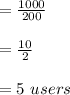
In Option b:

`\text{blocking probability} = \frac{link}{\text{1-Gbps} = 10^9 (bits)/(sec)}`

`\ let = 0.05 = (100)/(20) \\\\\text{blocking probability} = ( 200 * 10^6)/((100)/(20))`

`= ( 200 * 10^6 * 20 )/(100)\\\\= ( 2 * 10^6 * 20 )/(1)\\\\= 40 * 10^6 \\\\`

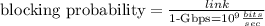
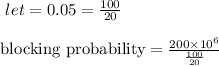
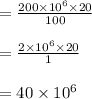
mean user
`= 25 * (1)/(20) \\\\`

`= 1.25`

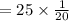
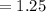
max user
`= (10^9)/(40 * 10^6) \\\\`

`= (10^9)/(4 * 10^7) \\\\ = (10^2)/(4) \\\\ = (100)/(4) \\\\= 25 \\\\ =\ \ 1 \ \ block \\\\`