Question

Suppose that the height (in centimeters) of a candle is a linear function of the amount of time (in hours) it has been burning. After 10 hours of burning, a candle has a height of 17 centimeters. After 21 hours of burning, its height is 12.6 centimeters. What is the height of the candle after 14 hours?

Answer 1

The height of the candle after 14 hours is 15.4 centimeters

Explanation:

A linear function is a polynomial function of the first degree of the form:

f(x)= m*x + b or y= m*x + b

where m is the slope of the function and b is the ordinate at the the y-intercept.

In this case height=m*time + b

Given two points of the line, point 1 (x1, y1) and point 2 (x2, y2), we can find the equation of the line or linear function.

You must first find the slope of the line using the expression:

`m=(y2 - y1)/(x2 - x1)`

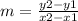
In this case you know the two points are (x1, y1)= (10,17) and (x2, y2)=(21,12.6)

So the slope is:

`m=(12.6-17)/(21-10)`

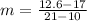
m= -0.4

Now you find the value of b, replacing m in the equation, the values ​​of x and y by the values ​​of the coordinates of one of the points and solving for b to obtain its value.

Replacing (x1, y1)= (10,17) and m=-0.4 in the expresion y=m*x+b:

17= -0.4*10 + b

and solving you get:

17= -4 + b

17 + 4= b

21= b

So: height= -0.4*time + 21 where the height is expressed in centimeters and the time in hours.

To calculate the height of the candle after 14 hours, you simply replace the time by 14:

height= -0.4*14 + 21

height= 15.4

The height of the candle after 14 hours is 15.4 centimeters